Frequency Therapeutics — Hearing Loss Regeneration

[Tezcatlipoca]

Yep, that's accurate and my understanding. The entire reason for priority dates is to act as a method of marking when you have approached the patent organizations that support filing claims, and made "public" (I'll explain why in quotes) your IP or concept that you want to claim is your invention (usually either a method of use, composition of matter, conceptual/design or some other variation).

Then 18 months from the priority date, the actual patent ends up being "published" which is the true moment it is actually public and it is visible if you look in patent databases. This 18 months AIUI is intended to ensure that if simultaneously someone else was also patenting it, there's a time window to allow for other claimants to step forward.

Once something is "published" ie patent is still in application stage but has publication, it can act as "prior art", a way of saying in the future that your patent pre-dates a competitor patent. At this stage you cannot actually force cease and desist until patent is granted, but this stage is usually valuable from IP security point of view if you believe the claims have strong merit. This is also the stage at which you can continue to make adjustments so it's almost more valuable for acquisition or whatever purposes if the scope or some material issue needs to be addressed since once patents are "granted" and actually defensible from C&D point of view, they are locked to the "granted" scope and not flexible.

Hope this helps.

WIPO is great, means they effectively have global IP coverage here in all regions.

That was very informative, thank you!

 

[Aaron91]

So this is another useful graph from the patent because it elucidates more information on the individual patients from both groups, particularly those who fell outside of the definition of a "non-responder". As some of us have previously speculated from the breadcrumbs Frequency Therapeutics had given us, some patients (now known to be 3) had such high WR baseline scores (almost 50/50) that it was impossible to determine whether the treatment had any effect, if at all.

One of the main reasons I wanted to share this graph is that it is being used to argue the bear thesis. The bear thesis is that there is a clear difference in the original average baseline between the placebo group and the FX-322 group. You'll notice that 3/6 placebo patients had 45/50 + word scores, so similar to the three FX-322 patients on the very far right hand side of the graph.

So I think a fair analysis would be to start by cutting out those outliers on both sides, leaving us with the 6/6 responders (4 stat sig) for FX-322 and 2/3 responders for placebo. This is the bear thesis: that 2/3 placebo patients who had headroom for improvement improved (they kind of gloss over by how much). Not only that, but those 2/3 placebo patients still had much higher baselines. These are fair points, but in my view only go so far.

I have two-counter arguments to this. Firstly, it is possible that one may not need a super low baseline such as that seen in the FX-322 patients to actually have the headroom needed for clinically meaningful improvement. We know that Frequency Therapeutics have drawn the line at <90% but we don't know whether that's at 60, 70 or 80%. My second point is more nuanced. The bear thesis looks at things from a group level, but I think it's important to also look at what's going on at an individual level. The 2/3 placebo patients improved less than 5 words (1 word and 4 words it would appear), even though they had the headroom to improve by about 10 and 6-7 words respectively. We know that Frequency Therapeutics counted 3/50 words as one standard deviation, although it remains unknown at how many standard deviations they drew a line for stat sig/CI (I'm wondering though if we can infer this somehow - @Zugzug you have a math background, right?). This is where things get a bit subjective, because depending on what audiology research you may read, you could draw that line arbitrarily at different points. In any case, the percentage improvement is very small in both patients. Compare that to the FX-322 respondents who improved from baseline by 24%, 32%, 68% , 76% , 78%, 94%.

Another reason why the bear thesis falls apart in my mind is because if this was placebo, then the chances are we would see something similar in Otonomy's work for OTO-413. These are slides from an Otonomy presentation but I feel they are relevant to Frequency Therapeutics.

As we all know Otonomy have a slightly different mechanism of action (synaptic repair as opposed to OHC repair), but the point here is that they too use an intratympanic injection and polymer gel as a form of delivery. You can see that they too have similar results against placebo. Most notably, there is not a single placebo responder. In Frequency Therapeutics there was 1/8 at day 15 and day 60 and 0/8 at day 90. But the fact you have the treatment groups responding in each clinical trial using the same delivery method tells me that the placebo is unlikely. Or to put it another way, the fact you have little and/or NO response in the placebo groups in both clinical trials (which use same placebo) tells me that this being explained by chance is unlikely.

In essence, I'm trying to see if this bear thesis has any weight and that we're not all suffering from confirmation bias. What do you guys think?

 

[Diesel]

Updated PHASE 2A 90-Day Expectations:

After reading through the recently shared International Patent application, and reviewing the other more recent sources, I'd like to share what would be my own expectations on the Phase 2A 90-Day readout. But first, a few thoughts on how Frequency Therapeutics recruited patients in the trial. I believe it was Carl LeBel and Chris Loose noted that for the Phase 2A, they were looking to recruit patients that matched more closely to the "Responders" that they discovered in the Phase 1/2. Carl LeBel further indicated in January, that Frequency Therapeutics did indeed have a secondary filter criteria that is currently a secret until the full results are released.

RECRUITING
I believe in addition to the Inclusion/Exclusion requirements on the Phase 2A Clinical Trial page, Frequency Therapeutics' additional filter criteria preferred that patients had:

- Asymmetric hearing loss
- Moderate to Moderately Severe Hearing Loss in the ear to be treated
- Mild hearing loss or no hearing loss in the untreated ear
- Tinnitus, but preferably only present in the ear to be treated
- Complaints of hearing-in-noise difficulty
- 4+ years with a hearing loss diagnosis, no less
- Approval by patient to treat the "worse ear" during the trial

So, I believe that the majority of the patients packed into these 4 groups probably fit the above criteria. And since they have a lot of room for improvement, and can show significant outcomes from treating a single bad ear, we should see clearly defined outcomes at the group average level. Note: I believe a patient with a bad ear + good ear, where the bad ear is treated should demonstrate a real-world 2-ear outcome better than a patient with 2 bad ears, where only 1 bad ear is treated. Especially for tinnitus. (Hope that makes sense).

EXPECTED OUTCOMES PER DOSE LEVEL AT 90-DAYS
Note: Since these are group averages, we cannot know statistical significance of the outcomes.
Note: Frequency Therapeutics plans to show Audiogram improvement in terms of a % improvement and an average threshold value. So, we should see how the group's threshold improved on an audiogram for both Standard + EHF ranges.

PLACEBO GROUP:
I don't expect placebo effect to be a factor at 90-days. They will all be unchanged by 90-days.

1X GROUP: (24 patients)
Word Recognition:

• 100% improvement over baseline on average (doubles).

WIN Recognition:

• 20% improvement over baseline on average.

Standard Audiogram:

• 5-10 dB improvement at 8 kHz on average. (All may not improve, so that will draw the average down).

EHF Audiogram:

• Average 9 kHz-16 kHz reading shows improvements to mild thresholds.

TFI:

• 7 point improvement on average.

2X GROUP:
Word Recognition:

• 100% improvement over group baseline.

WIN Recognition:

• 30% improvement over group baseline.

Standard Audiogram:

• 20 dB+ improvement at 8 kHz, average threshold may improve to mild.
• 5-10 dB improvement at 6 kHz, on average. Threshold may improve to moderate average.

EHF Audiogram:

• Average 9 kHz-16 kHz reading shows improvements to mild/normal thresholds.

TFI:

• 10 point improvement on average.

4X GROUP:
Word Recognition:

• 100% improvement over group baseline.

WIN Recognition:

• 40% improvement over group baseline.

Standard Audiogram:

• 30 dB+ improvement at 8 kHz, average threshold may improve to normal.
• 10 dB+ improvement at 6 kHz on average. Threshold may improve to mild average.
• 5-10 dB improvement at 4 kHz possible.

EHF Audiogram:

• Average 9 kHz-16 kHz reading shows improvements to normal thresholds.

TFI:

• 20 point improvement on average.

 

[Aaron91]

Analysis, Part I

So I ran a Fisher's Exact Test for myself on this test and computed the p-value. I was lazy so I just used Graphpad to do the calculations for me.

Assumptions:

• Two categorical variables: Variable 1 is Treatment (FX-322 or Placebo) and Variable 2 is Responder (Yes or No, where Yes means >5 dB at 6 and 8 kHz on day 90). This creates a 2x2 grid where the n=23 total sample size will satisfy that each patient lands in exactly 1 of the 4 cells.
• One-tailed test. In other words, the p-value looks for the "improvement" from FX-322 being at least as extreme. This means that I am looking for the probability that with 15 treated ears, 8 placebo ears, what is the probability that at least 2/15 ears will be a responder? Obviously, the p-value should be large, which is considered less evidence. A small p-value means that the probability of improvement at that level of extremeness if the null hypothesis (no improvement) was true, is small. Therefore, the closer p is to 0, the better and the closer p is to 1 (100%), the worse. Small p-values mean that the null hypothesis is harder to believe, essentially. Opposite for large p-values.

Notes:

• They performed this same test on the 6/15 responders to look for statistical significance. Therefore, it's a very reasonable test. They also performed a one-tailed test.

Results:
After a bunch of math, p=0.415. For some interpretation, we need p < .05 to be considered statistically significant. Also, note that p=.05 for the same test, but with "Responder" only requiring >5 dB improvement at 8 kHz. As we can see, big difference in the p-value.

This small sample sized, crude test tells me something pretty big. That is, 8 kHz is right around the boundary where drug action reaches. It is nice that 2/15 saw improvement at 6 kHz, but I think our expectations should be low. Moreover, to @Aaron91's point about the impact of dosing volume being similar because of Pick's law, that makes me think that the best we'll see from multiple dosing cohorts is added improvement at 8 kHz. I expect that 6/15 ratio to improve, but the 2/15 ratio at 6 kHz to barely improve in the Phase 2a study.

tl;dr: they need a new formulation or a fundamentally different drug delivery technique to reach lower. Still encouraging.

Analysis, Part II

I ran the same test as above, but with "Responder" changing to "tinnitus improvement" (Yes or No). My conservative assumption is that of the n=23 people in the study, there were only 3 tinnitus improvers in total. The only 3 tinnitus improvers came from the 15 treated ears.

The same one-tailed test procedure reveals a p-value of p=0.2569. For the two-tailed test (more conservative p-value, which considers the possibility that the drug worsened tinnitus), we have p=0.5257.

Caveats: This assumes that tinnitus was perfectly assessed and that only 3 people in the whole study improved. I have no idea is is true or not. Either way, it seems like if the 3 tinnitus responders came from the 6 responders, that's not bad for one dose.

@Zugzug This is great work. I'm just wondering whether it would be worth running these tests again while refining the definition of a responder under similar terms as to Frequency Therapeutics', which included the WR scores, so something to this effect:

"A responder definition was created while blinded that required both an improvement in audiometry (>5dB at 6kHz and 8 kHz) and a functional hearing improvement in either WR or WIN (>10%) compared to baseline".

This isn't the original definition as I added the 6 kHz in, but would this even be an exercise worth doing? I imagine we would need more complete data because we don't know whether those 2 patients who had improvements at 6 kHz also had improved WR scores - I'm digging through the patent to find out now. I may be wrong here, but I recall reading somewhere that those patients who did have the 8 kHz gains also had WR improvements, so I'm presuming those 2 patients must have been responders under the refined definition I've proposed above.

Edit: I just realised that this would reduce the sample size down to 2, in which case I guess you can't glean anything from it...

 

[rid0871]

I'm so tired of waiting on Frequency Therapeutics. If they have something that will help millions and millions, then they should help us. Sorry for venting. My ears are getting so bad...

 

[Diesel]

Analysis, Part I

So I ran a Fisher's Exact Test for myself on this test and computed the p-value. I was lazy so I just used Graphpad to do the calculations for me.

Assumptions:

• Two categorical variables: Variable 1 is Treatment (FX-322 or Placebo) and Variable 2 is Responder (Yes or No, where Yes means >5 dB at 6 and 8 kHz on day 90). This creates a 2x2 grid where the n=23 total sample size will satisfy that each patient lands in exactly 1 of the 4 cells.
• One-tailed test. In other words, the p-value looks for the "improvement" from FX-322 being at least as extreme. This means that I am looking for the probability that with 15 treated ears, 8 placebo ears, what is the probability that at least 2/15 ears will be a responder? Obviously, the p-value should be large, which is considered less evidence. A small p-value means that the probability of improvement at that level of extremeness if the null hypothesis (no improvement) was true, is small. Therefore, the closer p is to 0, the better and the closer p is to 1 (100%), the worse. Small p-values mean that the null hypothesis is harder to believe, essentially. Opposite for large p-values.

Notes:

• They performed this same test on the 6/15 responders to look for statistical significance. Therefore, it's a very reasonable test. They also performed a one-tailed test.

Results:
After a bunch of math, p=0.415. For some interpretation, we need p < .05 to be considered statistically significant. Also, note that p=.05 for the same test, but with "Responder" only requiring >5 dB improvement at 8 kHz. As we can see, big difference in the p-value.

This small sample sized, crude test tells me something pretty big. That is, 8 kHz is right around the boundary where drug action reaches. It is nice that 2/15 saw improvement at 6 kHz, but I think our expectations should be low. Moreover, to @Aaron91's point about the impact of dosing volume being similar because of Pick's law, that makes me think that the best we'll see from multiple dosing cohorts is added improvement at 8 kHz. I expect that 6/15 ratio to improve, but the 2/15 ratio at 6 kHz to barely improve in the Phase 2a study.

tl;dr: they need a new formulation or a fundamentally different drug delivery technique to reach lower. Still encouraging.

Analysis, Part II

I ran the same test as above, but with "Responder" changing to "tinnitus improvement" (Yes or No). My conservative assumption is that of the n=23 people in the study, there were only 3 tinnitus improvers in total. The only 3 tinnitus improvers came from the 15 treated ears.

The same one-tailed test procedure reveals a p-value of p=0.2569. For the two-tailed test (more conservative p-value, which considers the possibility that the drug worsened tinnitus), we have p=0.5257.

Caveats: This assumes that tinnitus was perfectly assessed and that only 3 people in the whole study improved. I have no idea is is true or not. Either way, it seems like if the 3 tinnitus responders came from the 6 responders, that's not bad for one dose.

Awesome work, my friend!

One thing they have never revealed was the baseline data of any of the responders for the audiogram and tinnitus. So, what we need to consider is, in the Phase 2A, they may have very well tried to stack the trial with 95 patients that had baselines/conditions similar to that group of responders. I wonder if we could, just for time-wasting's sake, simulate a series of 24 responders with random data responder-like baselines. #TimeWasting.

 

[grate_biff]

I'm so tired of waiting on Frequency Therapeutics. If they have something that will help millions and millions, then they should help us. Sorry for venting. My ears are getting so bad...

Your ears got bad from a neck adjustment?

 

[Keith Handy]

I would just like to note at this point that overanalysis of 6 kHz & 8 kHz data is like trying to write a thesis on elephants while having only ever observed an elephant's tail... when you're about to see a whole elephant for the first time in less than two weeks.

EHF readouts, baby. That's where daddy's money is*.

(*I have neither children nor money, but I reserve the right to use silly expressions whenever I have a moment of hope.)

 

[patorjk]

In essence, I'm trying to see if this bear thesis has any weight and that we're not all suffering from confirmation bias. What do you guys think?

Reading her bear thesis last night spiked my blood pressure and I had trouble sleeping. It would be pretty crushing if FX-322 failed to deliver after all of this time. She and her friends have done a pretty good job combing through the details of the study and finding things to pick apart.

However, it wasn't enough to break my confidence, though part of that is because I've been following this thread so closely and know many of the details very well. The WR score stuff alone is enough to give me confidence. I can't access the Twitter thread from where I am now, but I was the one who shared the chart you showed. It was in response to the one she shared about audiogram scores (though maybe it was shared elsewhere in the thread too). I wasn't sharing it to add to her thesis but to show that the placebo responders only barely made the cut.

 

[FGG]

Analysis, Part I

So I ran a Fisher's Exact Test for myself on this test and computed the p-value. I was lazy so I just used Graphpad to do the calculations for me.

Assumptions:

• Two categorical variables: Variable 1 is Treatment (FX-322 or Placebo) and Variable 2 is Responder (Yes or No, where Yes means >5 dB at 6 and 8 kHz on day 90). This creates a 2x2 grid where the n=23 total sample size will satisfy that each patient lands in exactly 1 of the 4 cells.
• One-tailed test. In other words, the p-value looks for the "improvement" from FX-322 being at least as extreme. This means that I am looking for the probability that with 15 treated ears, 8 placebo ears, what is the probability that at least 2/15 ears will be a responder? Obviously, the p-value should be large, which is considered less evidence. A small p-value means that the probability of improvement at that level of extremeness if the null hypothesis (no improvement) was true, is small. Therefore, the closer p is to 0, the better and the closer p is to 1 (100%), the worse. Small p-values mean that the null hypothesis is harder to believe, essentially. Opposite for large p-values.

Notes:

• They performed this same test on the 6/15 responders to look for statistical significance. Therefore, it's a very reasonable test. They also performed a one-tailed test.

Results:
After a bunch of math, p=0.415. For some interpretation, we need p < .05 to be considered statistically significant. Also, note that p=.05 for the same test, but with "Responder" only requiring >5 dB improvement at 8 kHz. As we can see, big difference in the p-value.

This small sample sized, crude test tells me something pretty big. That is, 8 kHz is right around the boundary where drug action reaches. It is nice that 2/15 saw improvement at 6 kHz, but I think our expectations should be low. Moreover, to @Aaron91's point about the impact of dosing volume being similar because of Pick's law, that makes me think that the best we'll see from multiple dosing cohorts is added improvement at 8 kHz. I expect that 6/15 ratio to improve, but the 2/15 ratio at 6 kHz to barely improve in the Phase 2a study.

tl;dr: they need a new formulation or a fundamentally different drug delivery technique to reach lower. Still encouraging.

Analysis, Part II

I ran the same test as above, but with "Responder" changing to "tinnitus improvement" (Yes or No). My conservative assumption is that of the n=23 people in the study, there were only 3 tinnitus improvers in total. The only 3 tinnitus improvers came from the 15 treated ears.

The same one-tailed test procedure reveals a p-value of p=0.2569. For the two-tailed test (more conservative p-value, which considers the possibility that the drug worsened tinnitus), we have p=0.5257.

Caveats: This assumes that tinnitus was perfectly assessed and that only 3 people in the whole study improved. I have no idea is is true or not. Either way, it seems like if the 3 tinnitus responders came from the 6 responders, that's not bad for one dose.

This is really interesting, but I have to question two assumptions:

One is: that improvements will only be 5 dB in the 6khz range even with multiple dosing. I think if the drug makes it at all, there would be greater effects with each subsequent dose.

There is a factor beyond just transport mechanics and that is how much of the drug gets "used up" along the way. The Phase 2a results and especially the EHF audiogram results should shed light on this.

The second is that we can apply statistics to the 50% of tinnitus responders without more detailed history. I think it's extremely telling that these were the same patients with large word score increases. In other words, the responders likely had worse EHF hearing loss and their tinnitus was concentrated in that range.

 

[Aaron91]

Reading her bear thesis last night spiked my blood pressure and I had trouble sleeping. It would be pretty crushing if FX-322 failed to deliver after all of this time. She and her friends have done a pretty good job combing through the details of the study and finding things to pick apart.

However, it wasn't enough to break my confidence, though part of that is because I've been following this thread so closely and know many of the details very well. The WR score stuff alone is enough to give me confidence. I can't access the Twitter thread from where I am now, but I was the one who shared the chart you showed. It was in response to the one she shared about audiogram scores (though maybe it was shared elsewhere in the thread too). I wasn't sharing it to add to her thesis but to show that the placebo responders only barely made the cut.

Funny you should mention that, I couldn't sleep either after that exchange and I feel like a zombie today.

In any case I'm glad you shared the chart. The last thing I want is for any us to stick our head in the sand, have false expectations and all end up with heartbreak. I've been combing through all the data again and I have to say although I'm still bullish about the data coming out of the trial because of how they will have improved its design, I'm a little less confident about what it will do for those of us with either mild hearing loss and/or hidden hearing loss. See graph below:

So this graph shows who the responders and non-responders were according to severity, along with where those responders' baseline WR scores were. You'll notice that most of the non-responders are in the mild group. We suspected this, but I think this is the first time I've seen a graph to confirm it. We can see from the WR scores that there was indeed a ceiling effect for the mild group. What's slightly disconcerting is that given FX-322's mechanism is to restore hair cells, and given that we also know from pharmacodynamic models that concentrations are mainly in the EHF region, and given that the literature suggests that OHCs responsible for EHF are the first to go, it would be reasonable to suggest that these patients have not improved their WR scores in spite of improvements in their EHF hearing. This can only mean one of three things:

1) The non-responders had disproportionate amounts of hearing loss in lower frequencies but better hearing in EHF while responders had greater losses up to 8 kHz but presumably much better hearing in EHF. I personally think this is impossible for several reasons. Firstly, we suspect that the responders responded because of gains in EHF. Secondly, it just doesn't match up with the literature. We know from the literature that the high frequencies are the first go and the lower frequencies can take a lot of wear and tear. So I personally think there is no way this is a plausible explanation.

2) The patients in the mild group have mostly synaptopathy, not hair cell loss. In which case, FX-322 would do very little for them.

3) Placebo (and therefore the trial/data is void). This is possible, but all the pre-clinical data and other smoking guns from Phase 1 would suggest this just isn't the case either.

So I'm inclined to go with option 2. This would also be consistent with the literature because IIRC Liberman has shown that synapses are the first to go and much more prone to damage/injury than hair cells. As someone with a pretty decent standard audiogram but who struggles with clarity, tinnitus and hyperacusis, this is deflating to say the least.

From a trial results point of view though, I think Frequency Therapeutics will have covered themselves with the lower WR scores.

Edit: I forget to recall my own criticism of this, which is that the mild group WR scores still had that ceiling. I think what I need to be looking at more closely is how those mild patients performed in noise.

Edit 2: Same thing happening in noise too. See graph below.

 

[Zugzug]

So this is another useful graph from the patent because it elucidates more information on the individual patients from both groups, particularly those who fell outside of the definition of a "non-responder". As some of us have previously speculated from the breadcrumbs Frequency Therapeutics had given us, some patients (now known to be 3) had such high WR baseline scores (almost 50/50) that it was impossible to determine whether the treatment had any effect, if at all.

One of the main reasons I wanted to share this graph is that it is being used to argue the bear thesis. The bear thesis is that there is a clear difference in the original average baseline between the placebo group and the FX-322 group. You'll notice that 3/6 placebo patients had 45/50 + word scores, so similar to the three FX-322 patients on the very far right hand side of the graph.

So I think a fair analysis would be to start by cutting out those outliers on both sides, leaving us with the 6/6 responders (4 stat sig) for FX-322 and 2/3 responders for placebo. This is the bear thesis: that 2/3 placebo patients who had headroom for improvement improved (they kind of gloss over by how much). Not only that, but those 2/3 placebo patients still had much higher baselines. These are fair points, but in my view only go so far.

I have two-counter arguments to this. Firstly, it is possible that one may not need a super low baseline such as that seen in the FX-322 patients to actually have the headroom needed for clinically meaningful improvement. We know that Frequency have drawn the line at <90% but we don't know whether that's at 60, 70 or 80%. My second point is more nuanced. The bear thesis looks at things from a group level, but I think it's important to also look at what's going on at an individual level. The 2/3 placebo patients improved less than 5 words (1 word and 4 words it would appear), even though they had the headroom to improve by about 10 and 6-7 words respectively. We know that frequency counted 3/50 words as one standard deviation, although it remains unknown at how many standard deviations they drew a line for stat sig/CI (I'm wondering though if we can infer this somehow - @Zugzug you have a math background, right?). This is where things get a bit subjective, because depending on what audiology research you may read, you could draw that line arbitrarily at different points. In any case, the percentage improvement is very small in both patients. Compare that to the FX-322 respondents who improved from baseline by 24%, 32%, 68% , 76% , 78%, 94%.

Okay, warning. This is going to majorly nerd out. I have studied this in great detail, aided by years of math research experience. @Aaron91, you bring up a great discussion, but I think you may be missing a few things. This post is broken into varying degrees of technical analysis. I will often refer to the attached Figure A. The vertical line is placed at the baseline 90% mark (45/50). Only data to the left of the line are considered.

Less Technical



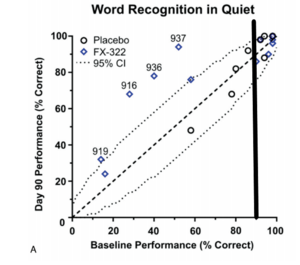
Firstly, in the published paper, they mention that of the n=23 ears, a total of 10 ears (<= 90% baseline) were eligible (Section Human Hearing Assessment and Outcomes). This 10 then split further into 6 FX-322 and 4 placebo. So the nontechnical analysis is that 4/6 FX-322 ears showed clinically meaningful improvements (two-sided test at 5% significance level, per Thornton and Raffin, 1978). None of the 4 placebo ears reached this mark.

The bear thesis points out that the 6 eligible FX-322 ears sit lower than the 4 eligible placebo ears. This is imbalanced data and occurs by chance. The <=90% requirement was set pre study and everything was selected at random. It's just sort of unfortunate. I won't comment on the group level comparisons because the fine details are not disclosed (that I can see) in the patent submission. I do understand the individual statistics very well, even down the nitty gritty of how the Thornton and Raffin 95% confidence intervals are derived and why it is justified (will be discussed down below).

As we can see from the figure, 2/4 of the placebos retested below the y=x line (same performance at baseline and day 90) and 2/4 rested above. Of note, the 2 that worsened started with lower baselines than the 2 who improved. So the theory that the only reason the 4 responders came from FX-322 is "low starting baselines" is at least somewhat tenuous since the placebo improvers started with higher scores.

In summary, 4/6 FX-322 eligible ears saw clinical significance and 2-sided statistical significance (at alpha=.05 significance level) per Thornton and Raffin. For placebo ears, this became 0/4.

More Technical

Without any derivations, what is a 2-sided 95% confidence interval and what does it mean here? Why is a 2-sided more conservative than a 1-sided confidence interval?

In layman's terms, a 95% confidence interval for an unknown population parameter (in this case the parameter is re-test percentage score) is an interval of the form (L,U), where L is the lower bound and U is the upper bound, such that if the experiment was repeated indefinitely, 95% of the time, if it really was the same experiment (i.e. no drugs, same testing conditions, etc.), the re-rest score would land in that interval. Essentially, "statistical significance" means that the re-rest score landed outside that interval, which means that although there's a chance it happened at random, there's statistical reason to believe that the experiments really were different (i.e. the drug did something).

Okay, so what's with this 2-sided vs 1-sided business? Note that in the Figure A, the dotted lines above and below the dashed line represent the L and U of what I described in the paragraph above. This is 2-sided because one can fall outside of the confidence from above or below.

A 2-sided test is more conservative because it assumes that worsening is possible. In other words, to clear the upper mark, U (obviously the goal is to see noteworthy improvements) requires more evidence. On the other hand, a 1-sided test would be only looking for improvement. In this case, in Figure A, the lower dotted curve (L) would be gone and the upper dotted curve (U) would be shifted down. In other words, it would be easier for the participants to clear the line, indicating statistical significance.

Anyways, this is what they mean when they show the 4 FX-322 ears above the dotted line.

Some natural thoughts may come to mind. We can say someone saw statistically significant improvement or that they didn't. But what's actually the case? Obviously, data is random and there's no way of knowing their true word score due to limitations in sample size. Hence, we could be right or wrong.

Being wrong in the "false positive" sense is called a type I error. This is worse because it's saying someone improved when they didn't. Imagine approving an ineffective or even unsafe drug. Big problems.

A "false negative" is called a type II error. This is when we say the null hypothesis could be true (i.e. no improvement) when actual improvement did occur. Though still undesirable, this error is preferred. Both errors are possible in any study and it has nothing at all to do with incompetence. It's kind of the point of statistical inference.

I won't get into it, but there's all kind of analysis on sample size, what's called "statistical power", and setting up the experiment to control Type I and Type II errors. Perhaps unsurprisingly, they are inversely related because they are opposite ideas. If one lowers the significance level, they make it harder to prove efficacy, but reduce Type I errors. This raises the chances of a Type II error.

To understand this, think of an extreme example. Say they were 99.9% confidence intervals (alpha=.001, very small). It would be very hard to prove statistical significance and we would essentially never reject the null hypothesis. The whole process is a balancing act. They want the drug approved, have a vision going in as to what the results would be, but have to test as if they don't know and that even a worsening could occur.

Much More Technical

What is it that Thornton and Raffin do to come up with the 95% WR confidence intervals for test-retest?

Think of it like this. Say I take the test twice. Let's assume that my performance is modeled by a Binomial Distribution (i.e. trials (words) are independent and I have the same probability at getting each word right (which depends on my hearing ability)).

The problem with test-retesting is that we don't know my true success rate, p. Say I take the test at baseline and have p=50% success rate. Then at 90 days, I do it again and score p=52% success rate. What is my true p? If I took the test hundreds of times, what would my p converge to?

Okay, so by the Law of Large Numbers, if I answer a certain number of words, my percentage score should get closer and closer to my true score. Let's assume that after I answered 50 words on 2 separate tests, my true percentage is almost known.

Then through some fancy math, we can justify a "variance stabilizing" angular transform (Freeman and Tukey, 1950). To put a long story short, the reason why this is done is because the fact that we don't know the true score produces vast differences in the 95% error margin size based on which p we pick.

This gives us the confidence that it doesn't matter if we didn't quite capture the true p. We can safely perform hypothesis testing with the 95% confidence interval and it's pretty reliable.

If the WR scores do not follow a binomial distribution (which they don't perfectly, as some words are harder than others), this method is somewhat flawed. However, it's pretty reasonable assumption. Thornton and Raffin actually looked at this in the first part of the paper.

For the group level stuff, I really want to know more, but they don't disclose which test they did other than say it's a MMRM (Mixed Model for Repeated Measures) approach. I hope to learn more about this at some point.

 

[Chetan]

View attachment 44080

So this is another useful graph from the patent because it elucidates more information on the individual patients from both groups, particularly those who fell outside of the definition of a "non-responder". As some of us have previously speculated from the breadcrumbs Frequency Therapeutics had given us, some patients (now known to be 3) had such high WR baseline scores (almost 50/50) that it was impossible to determine whether the treatment had any effect, if at all.....

In essence, I'm trying to see if this bear thesis has any weight and that we're not all suffering from confirmation bias. What do you guys think?

20Q: Word Recognition Testing - Let's Just Agree to do it Right!

You use the chart on this by looking at baseline score and looking at range for 50w or 25w test to determine if new score is stat sig change.

The 6% or 3 word isn't a std dev AIUI, it's the expected variance if you test and re-test patients over and over, a range of about 3 words that on average may change, that's it.

Hence why clinically meaningful is 10% improvement (5 words, hence just 1 word more than variance isn't enough, need at least 2 words beyond variance expected).

Someone else mentioned we need baseline info for responders/non-responders, I think your chart shows this right?

 

[Zugzug]

There is a factor beyond just transport mechanics and that is how much of the drug gets "used up" along the way. The Phase 2a results and especially the EHF audiogram results should shed light on this.

Very good point. If I understand the idea of what you're saying, it's that if I take a drug, though the half-life elimination rate is roughly fixed, the efficacy per amount improves with time. This is definitely true and if I understand correctly, a lot of how drugs work. For example, if I take an Ibuprofen, I am "overdosing" because a bunch will be metabolized, but what remains after a while is more effective. Is that the idea?

The second is that we can apply statistics to the 50% of tinnitus responders without more detailed history. I think it's extremely telling that these were the same patients with large word score increases. In other words, the responders likely had worse EHF hearing loss and their tinnitus was concentrated in that range.

Completely agree. Actually, I nearly had a part III exploring this very thing. I didn't know a great way of studying it with such small sample sizes.

The message is clear though. Responders respond and it's not a mistake.

 

[FGG]

Reading her bear thesis last night spiked my blood pressure and I had trouble sleeping. It would be pretty crushing if FX-322 failed to deliver after all of this time. She and her friends have done a pretty good job combing through the details of the study and finding things to pick apart.

However, it wasn't enough to break my confidence, though part of that is because I've been following this thread so closely and know many of the details very well. The WR score stuff alone is enough to give me confidence. I can't access the Twitter thread from where I am now, but I was the one who shared the chart you showed. It was in response to the one she shared about audiogram scores (though maybe it was shared elsewhere in the thread too). I wasn't sharing it to add to her thesis but to show that the placebo responders only barely made the cut.

Something I have noticed for years (as a hobby biotech investor well before I needed to immerse myself in as deeply as I do now for my own health concerns) is that a lot of the bio twitterheads tend strongly towards being bearish by default because it makes them appear right more of the time. There are very, very few willing to look at new platforms with anything but extreme pessimism no matter what.

 

[Zugzug]

I would just like to note at this point that overanalysis of 6 kHz & 8 kHz data is like trying to write a thesis on elephants while having only ever observed an elephant's tail... when you're about to see a whole elephant for the first time in less than two weeks.

EHF readouts, baby. That's where daddy's money is*.

(*I have neither children nor money, but I reserve the right to use silly expressions whenever I have a moment of hope.)

Haha, 100% facts. I am learning the Phase 1b stuff in order to better understand the Phase 2a stuff.

You are absolutely right that the Phase 1 is largely a safety study.

 

[GBB]

A look at the shareholders of Frequency Therapeutics...

Interesting read.

What Is The Ownership Structure Like For Frequency Therapeutics, Inc. (NASDAQ:FREQ)?

Dude you keep posting things that are literally written by AI.

 

[FGG]

Very good point. If I understand the idea of what you're saying, it's that if I take a drug, though the half-life elimination rate is roughly fixed, the efficacy per amount improves with time. This is definitely true and if I understand correctly, a lot of how drugs work. For example, if I take an Ibuprofen, I am "overdosing" because a bunch will be metabolized, but what remains after a while is more effective. Is that the idea?

I was more thinking of drug activating cells upstream. This may even induce local changes that would affect diffusion.

 

[Aaron91]

Okay, warning. This is going to majorly nerd out. I have studied this in great detail, aided by years of math research experience. @Aaron91, you bring up a great discussion, but I think you may be missing a few things. This post is broken into varying degrees of technical analysis. I will often refer to the attached Figure A. The vertical line is placed at the baseline 90% mark (45/50). Only data to the left of the line are considered.

Less Technical

View attachment 44083

Firstly, in the published paper, they mention that of the n=23 ears, a total of 10 ears (<= 90% baseline) were eligible (Section Human Hearing Assessment and Outcomes). This 10 then split further into 6 FX-322 and 4 placebo. So the nontechnical analysis is that 4/6 FX-322 ears showed clinically meaningful improvements (two-sided test at 5% significance level, per Thornton and Raffin, 1978). None of the 4 placebo ears reached this mark.

The bear thesis points out that the 6 eligible FX-322 ears sit lower than the 4 eligible placebo ears. This is imbalanced data and occurs by chance. The <=90% requirement was set pre study and everything was selected at random. It's just sort of unfortunate. I won't comment on the group level comparisons because the fine details are not disclosed (that I can see) in the patent submission. I do understand the individual statistics very well, even down the nitty gritty of how the Thornton and Raffin 95% confidence intervals are derived and why it is justified (will be discussed down below).

As we can see from the figure, 2/4 of the placebos retested below the y=x line (same performance at baseline and day 90) and 2/4 rested above. Of note, the 2 that worsened started with lower baselines than the 2 who improved. So the theory that the only reason the 4 responders came from FX-322 is "low starting baselines" is at least somewhat tenuous since the placebo improvers started with higher scores.

In summary, 4/6 FX-322 eligible ears saw clinical significance and 2-sided statistical significance (at alpha=.05 significance level) per Thornton and Raffin. For placebo ears, this became 0/4.

More Technical

Without any derivations, what is a 2-sided 95% confidence interval and what does it mean here? Why is a 2-sided more conservative than a 1-sided confidence interval?

In layman's terms, a 95% confidence interval for an unknown population parameter (in this case the parameter is re-test percentage score) is an interval of the form (L,U), where L is the lower bound and U is the upper bound, such that if the experiment was repeated indefinitely, 95% of the time, if it really was the same experiment (i.e. no drugs, same testing conditions, etc.), the re-rest score would land in that interval. Essentially, "statistical significance" means that the re-rest score landed outside that interval, which means that although there's a chance it happened at random, there's statistical reason to believe that the experiments really were different (i.e. the drug did something).

Okay, so what's with this 2-sided vs 1-sided business? Note that in the Figure A, the dotted lines above and below the dashed line represent the L and U of what I described in the paragraph above. This is 2-sided because one can fall outside of the confidence from above or below.

A 2-sided test is more conservative because it assumes that worsening is possible. In other words, to clear the upper mark, U (obviously the goal is to see noteworthy improvements) requires more evidence. On the other hand, a 1-sided test would be only looking for improvement. In this case, in Figure A, the lower dotted curve (L) would be gone and the upper dotted curve (U) would be shifted down. In other words, it would be easier for the participants to clear the line, indicating statistical significance.

Anyways, this is what they mean when they show the 4 FX-322 ears above the dotted line.

Some natural thoughts may come to mind. We can say someone saw statistically significant improvement or that they didn't. But what's actually the case? Obviously, data is random and there's no way of knowing their true word score due to limitations in sample size. Hence, we could be right or wrong.

Being wrong in the "false positive" sense is called a type I error. This is worse because it's saying someone improved when they didn't. Imagine approving an ineffective or even unsafe drug. Big problems.

A "false negative" is called a type II error. This is when we say the null hypothesis could be true (i.e. no improvement) when actual improvement did occur. Though still undesirable, this error is preferred. Both errors are possible in any study and it has nothing at all to do with incompetence. It's kind of the point of statistical inference.

I won't get into it, but there's all kind of analysis on sample size, what's called "statistical power", and setting up the experiment to control Type I and Type II errors. Perhaps unsurprisingly, they are inversely related because they are opposite ideas. If one lowers the significance level, they make it harder to prove efficacy, but reduce Type I errors. This raises the chances of a Type II error.

To understand this, think of an extreme example. Say they were 99.9% confidence intervals (alpha=.001, very small). It would be very hard to prove statistical significance and we would essentially never reject the null hypothesis. The whole process is a balancing act. They want the drug approved, have a vision going in as to what the results would be, but have to test as if they don't know and that even a worsening could occur.

Much More Technical

What is it that Thornton and Raffin do to come up with the 95% WR confidence intervals for test-retest?

Think of it like this. Say I take the test twice. Let's assume that my performance is modeled by a Binomial Distribution (i.e. trials (words) are independent and I have the same probability at getting each word right (which depends on my hearing ability)).

The problem with test-retesting is that we don't know my true success rate, p. Say I take the test at baseline and have p=50% success rate. Then at 90 days, I do it again and score p=52% success rate. What is my true p? If I took the test hundreds of times, what would my p converge to?

Okay, so by the Law of Large Numbers, if I answer a certain number of words, my percentage score should get closer and closer to my true score. Let's assume that after I answered 50 words on 2 separate tests, my true percentage is almost known.

Then through some fancy math, we can justify a "variance stabilizing" angular transform (Freeman and Tukey, 1950). To put a long story short, the reason why this is done is because the fact that we don't know the true score produces vast differences in the 95% error margin size based on which p we pick.

This gives us the confidence that it doesn't matter if we didn't quite capture the true p. We can safely perform hypothesis testing with the 95% confidence interval and it's pretty reliable.

If the WR scores do not follow a binomial distribution (which they don't perfectly, as some words are harder than others), this method is somewhat flawed. However, it's pretty reasonable assumption. Thornton and Raffin actually looked at this in the first part of the paper.

For the group level stuff, I really want to know more, but they don't disclose which test they did other than say it's a MMRM (Mixed Model for Repeated Measures) approach. I hope to learn more about this at some point.

This is quite possibly my favourite post on Tinnitus Talk of all time. You are a credit to the community, @Zugzug.

Thankfully I did a module in stats in grad school so I was able to follow most of it. The most important takeaway for me was the 2-sided stat sig for 4/6 FX-322 eligible ears against the 0/4 per Thornton and Raffin. I think if the bears read this they may change their tune.

I'm now just trying to figure out what the data would show if it was a 1-sided test. Obviously the two placebo patients below the y = x line would no longer be relevant due to their worsening, but that then brings down our sample size. Is that an un-useful trade off?

I suppose this raises a clinical/qualitative question of whether a worsening is truly possible from an ITT injection (i.e. is any worsening from the procedure itself offset by the drug), but to your point, I guess this would put a smokescreen on any potential safety concerns. Am I right to take away from this is that two-sided tests must be pretty important for safety concerns, even though by introducing it there's a chance you may make the efficacy data look slightly "weaker"? I remember learning how to do both a one-sided and two-sided test, but I don't recall ever being given a practical example as to why a two-sided test could be quite critical in certain situations. If I'm not mistaken, this would appear to be one of them.

 

[Zugzug]

Reading her bear thesis

Who is her and what is her analysis?

 

[FGG]

EHF readouts, baby. That's where daddy's money is*.

(*I have neither children nor money, but I reserve the right to use silly expressions whenever I have a moment of hope.)

Anyone can be a "daddy". It's a state of mind!

 

[ThomasRobert]

Dude you keep posting things that are literally written by AI.

 

[Zugzug]

Me before following this thread:

Me after studying the papers:

 

[Zugzug]

@Zugzug This is great work. I'm just wondering whether it would be worth running these tests again while refining the definition of a responder under similar terms as to Frequency Therapeutics', which included the WR scores, so something to this effect:

"A responder definition was created while blinded that required both an improvement in audiometry (>5dB at 6kHz and 8 kHz) and a functional hearing improvement in either WR or WIN (>10%) compared to baseline".

This isn't the original definition as I added the 6 kHz in, but would this even be an exercise worth doing? I imagine we would need more complete data because we don't know whether those 2 patients who had improvements at 6 kHz also had improved WR scores - I'm digging through the patent to find out now. I may be wrong here, but I recall reading somewhere that those patients who did have the 8 kHz gains also had WR improvements, so I'm presuming those 2 patients must have been responders under the refined definition I've proposed above.

Edit: I just realised that this would reduce the sample size down to 2, in which case I guess you can't glean anything from it..

Yeah. What you are referring to boils down to the same test that I ran. The same people who are 6 kHz responders are 8 kHz responders and WR and SIN responders.

 

[FGG]

I wonder if we could, just for time-wasting's sake, simulate a series of 24 responders with random data responder-like baselines. #TimeWasting.

How would you do this?

 

[FGG]

Funny you should mention that, I couldn't sleep either after that exchange and I feel like a zombie today.

In any case I'm glad you shared the chart. The last thing I want is for any us to stick our head in the sand, have false expectations and all end up with heartbreak. I've been combing through all the data again and I have to say although I'm still bullish about the data coming out of the trial because of how they will have improved its design, I'm a little less confident about what it will do for those of us with either mild hearing loss and/or hidden hearing loss. See graph below:

View attachment 44084

So this graph shows who the responders and non-responders were according to severity, along with where those responders' baseline WR scores were. You'll notice that most of the non-responders are in the mild group. We suspected this, but I think this is the first time I've seen a graph to confirm it. We can see from the WR scores that there was indeed a ceiling effect for the mild group. What's slightly disconcerting is that given FX-322's mechanism is to restore hair cells, and given that we also know from pharmacodynamic models that concentrations are mainly in the EHF region, and given that the literature suggests that OHCs responsible for EHF are the first to go, it would be reasonable to suggest that these patients have not improved their WR scores in spite of improvements in their EHF hearing. This can only mean one of three things:

1) The non-responders had disproportionate amounts of hearing loss in lower frequencies but better hearing in EHF while responders had greater losses up to 8 kHz but presumably much better hearing in EHF. I personally think this is impossible for several reasons. Firstly, we suspect that the responders responded because of gains in EHF. Secondly, it just doesn't match up with the literature. We know from the literature that the high frequencies are the first go and the lower frequencies can take a lot of wear and tear. So I personally think there is no way this is a plausible explanation.

2) The patients in the mild group have mostly synaptopathy, not hair cell loss. In which case, FX-322 would do very little for them.

3) Placebo (and therefore the trial/data is void). This is possible, but all the pre-clinical data and other smoking guns from Phase 1 would suggest this just isn't the case either.

So I'm inclined to go with option 2. This would also be consistent with the literature because IIRC Liberman has shown that synapses are the first to go and much more prone to damage/injury than hair cells. As someone with a pretty decent standard audiogram but who struggles with clarity, tinnitus and hyperacusis, this is deflating to say the least.

From a trial results point of view though, I think Frequency Therapeutics will have covered themselves with the lower WR scores.

Edit: I forget to recall my own criticism of this, which is that the mild group WR scores still had that ceiling. I think what I need to be looking at more closely is how those mild patients performed in noise.

Edit 2: Same thing happening in noise too. See graph below.

View attachment 44089

EHF isn't always the first to go. It's just more common.

There are even people with profound standard audiogram losses with completely normal UHF audiograms (rare to be that extreme but it does happen. They have "unusually good speech" too.)

I don't think you can use the Phase 1 data/sample size to make any of those kind of inferences (though people with synaptopathy truly without any hair cell loss will need a synaptopathy drug but those were not included in the trial) but luckily we will have a lot more data soon.

 

[Zugzug]

This is quite possibly my favourite post on Tinnitus Talk of all time. You are a credit to the community, @Zugzug.

Thankfully I did a module in stats in grad school so I was able to follow most of it. The most important takeaway for me was the 2-sided stat sig for 4/6 FX-322 eligible ears against the 0/4 per Thornton and Raffin. I think if the bears read this they may change their tune.

I'm now just trying to figure out what the data would show if it was a 1-sided test. Obviously the two placebo patients below the y = x line would no longer be relevant due to their worsening, but that then brings down our sample size. Is that an un-useful trade off?

I suppose this raises a clinical/qualitative question of whether a worsening is truly possible from an ITT injection (i.e. is any worsening from the procedure itself offset by the drug), but to your point, I guess this would put a smokescreen on any potential safety concerns. Am I right to take away from this is that two-sided tests must be pretty important for safety concerns, even though by introducing it there's a chance you may make the efficacy data look slightly "weaker"? I remember learning how to do both a one-sided and two-sided test, but I don't recall ever being given a practical example as to why a two-sided test could be quite critical in certain situations. If I'm not mistaken, this would appear to be one of them.

So I guess I outlined the basic ideas behind one and two sided tests and their advantages. To be honest, I'm not an experienced statistician so am still learning about what people think about one and two sided tests in practice.

Some argue that two one-sided tests is fine and has the advantages of requiring a smaller sample size to demonstrate statistical power. Power (the probability of correctly demonstrating efficacy, often 80%) can be set based on what the researchers think could happen. Then they can guess the sample size required to achieve a certain level of statistical power.

I understand these ideas from a formulaic or mathematical perspective, but I don't have enough clinical experience. Of course, it depends on the drug and what likelihood of it being dangerous. It also depends on what's available. For example, if I have a super safe drug and there are no other treatments, intuitively, it seems like leaning less conservative could be more justified.

 

[Tezcatlipoca]

Weren't FX-322's synaptopathy outcomes basically identical to OTO-413's?

 

[FGG]

Weren't FX-322's synaptopathy outcomes basically identical to OTO-413's?

Not exactly. And the problem is the testing. It's likely "speech in noise" reflects both ultra high frequency hearing and synapse number.

 

[Tezcatlipoca]

Not exactly. And the problem is the testing. It's likely "speech in noise" reflects both ultra high frequency hearing and synapse number.

I see, but still, even the previous phase data shows improvements in those areas, right? Isn't that some evidence of effectiveness? And with long lasting beneficial effects.