Yes, there were speech in noise improvements if that's what you are asking. This doesn't mean it also treats "cochlear synaptopathy" though.I see, but still, even the previous phase data shows improvements in those areas, right? Isn't that some evidence of effectiveness? And with long lasting beneficial effects.
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Frequency Therapeutics — Hearing Loss Regeneration
- Thread starter RB2014
- Start date
More options
Who Replied?- Feb 14, 2020
- 1,630
- Tinnitus Since
- 1-2019
- Cause of Tinnitus
- 20+ Years of Live Music, Motorcycles, and Power Tools
1. Consider the entrance criteria for the responders.How would you do this?
Audiogram, incoming word score, win, asymmetric/symmetric hearing loss etc.
2. Note how the application of FX-322 improved these patients.
3. Create a model. Assume variances for improvement.
4. Create variations from this model based on real world examples (IE: moderate hearing loss audiograms, other research with similar data, etc)
5. Expand this model with synthethic patients.
6. Use the model + random variance assignment to the synthetic patient population.
I have said it before, and I'll say it again. Frequency Therapeutics just happened to get those 6 responders that we're analysing the shit out of. They learned that there is a "goldilocks" patient, that based on their hearing performance (audiogram, word score, win, other factors) make them really good entrants to the trial, and can give them the results they want to show efficacy. In the PHASE 2A, they stacked the statistical deck to get 96 patients that looked like those 6.
A model needs to be made assuming a population of 96 patients that look like those 6, and applies roughly how FX-322 helped those 6 to 96. Then, re-run the assessment.
Oh I didn't realize that, do we have any clue of what it could mean then? If not Cochlear Synaptopathy, then how did those improvements happen?Yes, there were speech in noise improvements if that's what you are asking. This doesn't mean it also treats "cochlear synaptopathy" though.
The only issue is we have no data of placebo patients that match the characteristics of those responders unfortunately (baseline scores etc), hence you can model the FX-322 groups potentially (though extrapolating multi-dose would be speculation imo given lack of data), but you can't model the placebo groups adequately (but can assume that the placebo response is minimal to assume some distribution of day 90 similar to Phase 1, but this may be false).1. Consider the entrance criteria for the responders.
Audiogram, incoming word score, win, asymmetric/symmetric hearing loss etc.
2. Note how the application of FX-322 improved these patients.
3. Create a model. Assume variances for improvement.
4. Create variations from this model based on real world examples (IE: moderate hearing loss audiograms, other research with similar data, etc)
5. Expand this model with synthethic patients.
6. Use the model + random variance assignment to the synthetic patient population.
I have said it before, and I'll say it again. Frequency Therapeutics just happened to get those 6 responders that we're analysing the shit out of. They learned that there is a "goldilocks" patient, that based on their hearing performance (audiogram, word score, win, other factors) make them really good entrants to the trial, and can give them the results they want to show efficacy. In the PHASE 2A, they stacked the statistical deck to get 96 patients that looked like those 6.
A model needs to be made assuming a population of 96 patients that look like those 6, and applies roughly how FX-322 helped those 6 to 96. Then, re-run the assessment.
Because speech in noise is effected by ultra high frequency hearing too according to Frequency Therapeutics.Oh I didn't realize that, do we have any clue of what it could mean then? If not Cochlear Synaptopathy, then how did those improvements happen?
- Feb 14, 2020
- 1,630
- Tinnitus Since
- 1-2019
- Cause of Tinnitus
- 20+ Years of Live Music, Motorcycles, and Power Tools
OOOHH... I get to use my graphic!Oh I didn't realize that, do we have any clue of what it could mean then? If not Cochlear Synaptopathy, then how did those improvements happen?
- Feb 14, 2020
- 1,630
- Tinnitus Since
- 1-2019
- Cause of Tinnitus
- 20+ Years of Live Music, Motorcycles, and Power Tools
Agree, partially. There would need to be some assumptions. So, a series of models would need to be created with the assumptions ON or OFF.The only issue is we have no data of placebo patients that match the characteristics of those responders unfortunately (baseline scores etc), hence you can model the FX-322 groups potentially (though extrapolating multi-dose would be speculation imo given lack of data), but you can't model the placebo groups adequately (but can assume that the placebo response is minimal to assume some distribution of day 90 similar to Phase 1, but this may be false).
I argue that you don't really need to know what the placebo group looked like; it was random assignment. They probably had similar hearing conditions as the responders and non-responders. The assumption is that their baseline didn't move enough to matter, so there would be a set placebo variables randomly assigned to those synthetic inputs that create movement of the outputs similar to the Phase 1/2.
I'm certainly happy to go deep into the rabbit hold of generating synthetic inputs and surrogate/agent outputs in a model based on limited data to understand how FX-322 might apply to a homogeneous population of 24 and/or 96 participants.
The biggest assumption, which we agree, is it the multi-dose variable. What does that next dose of FX-322 do inside the cochlea? If there's no exposed support cells to "absorb" at the high frequencies, does it keep dissipating until it hits damage further down?
- Aug 5, 2019
- 1,852
- Tinnitus Since
- 05/2019
- Cause of Tinnitus
- Autoimmune hyperacusis from Sjogren's Syndrome
1. Consider the entrance criteria for the responders.
Audiogram, incoming word score, win, asymmetric/symmetric hearing loss etc.
2. Note how the application of FX-322 improved these patients.
3. Create a model. Assume variances for improvement.
4. Create variations from this model based on real world examples (IE: moderate hearing loss audiograms, other research with similar data, etc)
5. Expand this model with synthethic patients.
6. Use the model + random variance assignment to the synthetic patient population.
I have said it before, and I'll say it again. Frequency Therapeutics just happened to get those 6 responders that we're analysing the shit out of. They learned that there is a "goldilocks" patient, that based on their hearing performance (audiogram, word score, win, other factors) make them really good entrants to the trial, and can give them the results they want to show efficacy. In the PHASE 2A, they stacked the statistical deck to get 96 patients that looked like those 6.
A model needs to be made assuming a population of 96 patients that look like those 6, and applies roughly how FX-322 helped those 6 to 96. Then, re-run the assessment.
What could be done, and this is so bullish it's almost a joke, is assume that the 6 responders accurately describe the distribution of the population under a similar filter. Assume they are able to recruit in such a way that they have no problems applying this filter to everyone.The only issue is we have no data of placebo patients that match the characteristics of those responders unfortunately (baseline scores etc), hence you can model the FX-322 groups potentially (though extrapolating multi-dose would be speculation imo given lack of data), but you can't model the placebo groups adequately (but can assume that the placebo response is minimal to assume some distribution of day 90 similar to Phase 1, but this may be false).
Then bootstrap with the 6 responders as the new population distribution.
Completely speculative to do this for group comparisons. Still bullish, but makes the most sense to only do this to the 1-dose cohort.
After doing this, we could all star in a Red Bull commercial, raising awareness for hearing disorders.
Oh that's true. They did say that. Good thing most of us have the most loss in those areas.Because speech in noise is effected by ultra high frequency hearing too according to Frequency Therapeutics.
- Feb 14, 2020
- 1,630
- Tinnitus Since
- 1-2019
- Cause of Tinnitus
- 20+ Years of Live Music, Motorcycles, and Power Tools
Winner winner.What could be done, and this is so bullish it's almost a joke, is assume that the 6 responders accurately describe the distribution of the population under a similar filter. Assume they are able to recruit in such a way that they have no problems applying this filter to everyone.
Then bootstrap with the 6 responders as the new population distribution.
Completely speculative to do this for group comparisons. Still bullish, but makes the most sense to only do this to the 1-dose cohort.
After doing this, we could all star in a Red Bull commercial, raising awareness for hearing disorders.
- Aug 5, 2019
- 1,852
- Tinnitus Since
- 05/2019
- Cause of Tinnitus
- Autoimmune hyperacusis from Sjogren's Syndrome
Here's one problem I thought of, thinking about my last post about it being bullish.I argue that you don't really need to know what the placebo group looked like; it was random assignment. They probably had similar hearing conditions as the responders and non-responders. The assumption is that their baseline didn't move enough to matter, so there would be a set placebo variables randomly assigned to those synthetic inputs that create movement of the outputs similar to the Phase 1/2.
Part of the reason why it's bullish is because, by chance, their data was imbalanced. In other words, it's a damn shame that the placebos had shifted up baselines so significantly (the risk of small sample sizes, unfortunately).
While I did make a compelling case above that there's something going on, it's kind of a nightmare to bootstrap from imbalanced data with small sample sizes lol. It really is such a shame that there aren't 4-5 more placebo baseline data points near the FX-322 responders.
Can't be avoided though, chance is a bitch. Chance is why we all have rare, messed up hearing problems.
- May 27, 2020
- 556
- Tinnitus Since
- 2007
- Cause of Tinnitus
- Loud music/headphones/concerts - Hyperacusis from motorbike
I'm sure this was implied although I'm not too sure it was clear, but for everyone else's sake, it needs to be said that we actually have no data on how many of those 23 patients had tinnitus to start with (if someone has data on this please let me know). It could have just been those 3 patients, it could have just been the 6 responders, or it could have been all 23 patients or any number in between. We just don't know. For Frequency Therapeutics to state in the patent, however, that 3 patients from the treatment group saw their tinnitus improve while "omitting" whether anyone from the placebo group also improved would seem to suggest to me that there was nothing to omit at all i.e. no one from the placebo group saw their tinnitus improve - assuming they even had tinnitus in the first place. The one thing we do know for sure though is this: at least half of the "respondents" in the treatment group (3/6), as defined by Frequency Therapeutics (for whatever that's worth), saw their tinnitus improve.Analysis, Part II
I ran the same test as above, but with "Responder" changing to "tinnitus improvement" (Yes or No). My conservative assumption is that of the n=23 people in the study, there were only 3 tinnitus improvers in total. The only 3 tinnitus improvers came from the 15 treated ears.
The same one-tailed test procedure reveals a p-value of p=0.2569. For the two-tailed test (more conservative p-value, which considers the possibility that the drug worsened tinnitus), we have p=0.5257.
Caveats: This assumes that tinnitus was perfectly assessed and that only 3 people in the whole study improved. I have no idea is is true or not. Either way, it seems like if the 3 tinnitus responders came from the 6 responders, that's not bad for one dose.
Keith Handy
Member
- Jan 5, 2021
- 302
- Tinnitus Since
- 11/2020
- Cause of Tinnitus
- Stress + sleep deprivation + noise
Bumping/amplifying the above question.So is there anything specifically that can identify if you have hair cell loss or synapse damage?
"FX-322 gives you ears!"After doing this, we could all star in a Red Bull commercial, raising awareness for hearing disorders.
- Feb 14, 2020
- 1,630
- Tinnitus Since
- 1-2019
- Cause of Tinnitus
- 20+ Years of Live Music, Motorcycles, and Power Tools
Why not just assume that 50% of the participants recruited in the Phase 2A had tinnitus in at least 1 ear?I'm sure this was implied although I'm not too sure it was clear, but for everyone else's sake, it needs to be said that we actually have no data on how many of those 23 patients had tinnitus to start with (if someone has data on this please let me know). It could have just been those 3 patients, it could have just been the 6 responders, or it could have been all 23 patients or any number in between. We just don't know. For Frequency Therapeutics to state in the patent, however, that 3 patients from the treatment group saw their tinnitus improve while "omitting" whether anyone from the placebo group also improved would seem to suggest to me that there was nothing to omit at all i.e. no one from the placebo group saw their tinnitus improve - assuming they even had tinnitus in the first place. The one thing we do know for sure though is this: at least half of the "respondents" in the treatment group (3/6), as defined by Frequency Therapeutics (for whatever that's worth), saw their tinnitus improve.
Audiograms can tell you if you have OHC damage if it's bad and widespread enough.Bumping/amplifying the above question.
Speech in Noise testing is correlated with synapse loss but there are other factors that can affect it, too (like ultra high frequency hearing).
Hearing regen is a weird area because good treatments may actually predate good diagnostics. A lot of people will probably have to "trial treat" their hearing issues in more subtle cases imo.
So what would sudden hearing loss with an audiogram of hearing loss starting at 5 kHz through 8 kHz around 65-70 dB with good word recognition and bad speech-in-noise in your opinion indicate?Audiograms can tell you if you have OHC damage if it's bad and widespread enough.
Speech in Noise testing is correlated with synapse loss but there are other factors that can affect it, too (like ultra high frequency hearing).
Hearing regen is a weird area because good treatments may actually predate good diagnostics. A lot of people will probably have to "trial treat" their hearing issues in more subtle cases imo.
- Aug 5, 2019
- 1,852
- Tinnitus Since
- 05/2019
- Cause of Tinnitus
- Autoimmune hyperacusis from Sjogren's Syndrome
Okay, here is my final deep dive post. I end up computing the 2-sided p-values for all 6 eligible FX-322 participants on the WR test-retest. Recall that 4/6 are statistically significant (and clinically) by the Thornton and Raffin 95% confidence intervals. Hence, we will have 4 individual p-values less than .05 and 2 greater than .05. Note that everyone saw improvement, even if it wasn't statistically significant. One non-significant person was right on the cusp of significant.
Background: I was thinking about the bear/bull divide and it occurred to me where it is. Roughly speaking, since the data was imbalanced by chance, the placebos started off closer to a ceiling effect. Hence, even though all group level differences were statistically significant, except PTA, the bears would argue that the placebos had a harder fight, with higher starting baselines -- probably some validity to this, even though it's percentage based.
But here's where the divide really is. Frequency Therapeutics have said (in the Tinnitus Talk Podcast) that there shouldn't really be a placebo effect with hearing words. Looking at the placebo patients, this is what we would expect. They all land in the 95% confidence intervals and scattered above and below.
The bulls think even with the data imbalance, let's focus on the responders. Placebo control is a little less important to us because we think the placebo effect is less for hearing. We see the 4 WR responders with massive gains and think that even though it's only 4, there's no way that's by chance or just retesting a little better. I think so much of the bull/bear position is what you think of a placebo effect. However, I do want to reiterate that the FX-322 group did outperform the placebo group in every test except one so it's not just zooming in on 4 ears.
Okay, here's my work and calculations from Thornton and Raffin. I am writing it out for completeness, but it's perfectly fine to skip right to the p-values. From the patent submission,
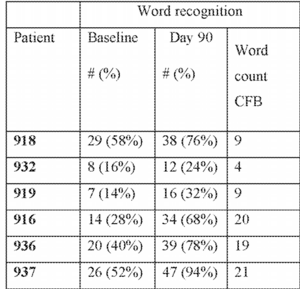
By Central Limit Theorem (justified), we apply angular transformations to baseline and day 90 scores. Then using the Freeman and Tukey uniform variance formula that was adjusted by Mosteller and Youtz (1961), we have the formula
Z=(arcsin(sqrt(x/(n+1)))+arcsin(sqrt((x+1)/(n+1)))-(arcsin(sqrt(y/(n+1)))+arcsin(sqrt((y+1)/(n+1))))/sqrt(2/(n+1/2)).
Here,
Patient 918: Z=-1.8972, p=2*P(Z<-1.8972)= 0.0578,
which is not less than alpha (but close) so not statistically significant.
Patient 932: Z=-0.9795, p=2*P(Z<-0.9795)= 0.3273,
which is not less than alpha and not close.
Patient 919: Z=-2.1268, p=2*P(Z<-2.1268)= 0.0334,
which is less than alpha so statistically significant.
Patient 916: Z=-4.0547, p=2*P(Z<-4.0547)= 0.00005,
which is way less than alpha so very statistically significant.
Patient 936: Z=-3.9133, p=2*P(Z<-3.9133)= 0.00009,
which is way less than alpha so very statistically significant.
Patient 937: Z=-5.0387, p=2*P(Z<-5.0387)= 0.00000047,
which is way less than alpha so very statistically significant.
So I will conclude with some commentary on these p-values. The last three (patients 916, 936, and 937) have very small p-values. It's even crazier because this is two-sided, which produces bigger p-values. The probability of that occurring by chance is practically impossible to believe.
Let's just say that I'm a bull and there are 3 patients in the Phase 1b study riding me hard.
Background: I was thinking about the bear/bull divide and it occurred to me where it is. Roughly speaking, since the data was imbalanced by chance, the placebos started off closer to a ceiling effect. Hence, even though all group level differences were statistically significant, except PTA, the bears would argue that the placebos had a harder fight, with higher starting baselines -- probably some validity to this, even though it's percentage based.
But here's where the divide really is. Frequency Therapeutics have said (in the Tinnitus Talk Podcast) that there shouldn't really be a placebo effect with hearing words. Looking at the placebo patients, this is what we would expect. They all land in the 95% confidence intervals and scattered above and below.
The bulls think even with the data imbalance, let's focus on the responders. Placebo control is a little less important to us because we think the placebo effect is less for hearing. We see the 4 WR responders with massive gains and think that even though it's only 4, there's no way that's by chance or just retesting a little better. I think so much of the bull/bear position is what you think of a placebo effect. However, I do want to reiterate that the FX-322 group did outperform the placebo group in every test except one so it's not just zooming in on 4 ears.
Okay, here's my work and calculations from Thornton and Raffin. I am writing it out for completeness, but it's perfectly fine to skip right to the p-values. From the patent submission,

By Central Limit Theorem (justified), we apply angular transformations to baseline and day 90 scores. Then using the Freeman and Tukey uniform variance formula that was adjusted by Mosteller and Youtz (1961), we have the formula
Z=(arcsin(sqrt(x/(n+1)))+arcsin(sqrt((x+1)/(n+1)))-(arcsin(sqrt(y/(n+1)))+arcsin(sqrt((y+1)/(n+1))))/sqrt(2/(n+1/2)).
Here,
- x=# correct out of 50 at baseline,
- y = # correct out of 50 at day 90,
- n=50
Patient 918: Z=-1.8972, p=2*P(Z<-1.8972)= 0.0578,
which is not less than alpha (but close) so not statistically significant.
Patient 932: Z=-0.9795, p=2*P(Z<-0.9795)= 0.3273,
which is not less than alpha and not close.
Patient 919: Z=-2.1268, p=2*P(Z<-2.1268)= 0.0334,
which is less than alpha so statistically significant.
Patient 916: Z=-4.0547, p=2*P(Z<-4.0547)= 0.00005,
which is way less than alpha so very statistically significant.
Patient 936: Z=-3.9133, p=2*P(Z<-3.9133)= 0.00009,
which is way less than alpha so very statistically significant.
Patient 937: Z=-5.0387, p=2*P(Z<-5.0387)= 0.00000047,
which is way less than alpha so very statistically significant.
So I will conclude with some commentary on these p-values. The last three (patients 916, 936, and 937) have very small p-values. It's even crazier because this is two-sided, which produces bigger p-values. The probability of that occurring by chance is practically impossible to believe.
Let's just say that I'm a bull and there are 3 patients in the Phase 1b study riding me hard.
Hello friends, anyone else notice that IBB and NASDAQ were both up today but FREQ continues to drop?
You have to wonder if some leaking is going on over there at headquarters and the news is not good. I'm desperate for a solution like the rest of you and have also accumulated 400 shares.
You have to wonder if some leaking is going on over there at headquarters and the news is not good. I'm desperate for a solution like the rest of you and have also accumulated 400 shares.
Is below 5 kHz completely normal? This could give you a better word score.So what would sudden hearing loss with an audiogram of hearing loss starting at 5 kHz through 8 kHz around 65-70 dB with good word recognition and bad speech-in-noise in your opinion indicate?
I think you likely have losses from 5 kHz all the way up. Your UHF hearing is involved in speech in noise, too, so you don't necessarily need synaptopathy to explain it in your case imo.
- May 27, 2020
- 556
- Tinnitus Since
- 2007
- Cause of Tinnitus
- Loud music/headphones/concerts - Hyperacusis from motorbike
I wasn't talking about Phase 2a... am I missing something? I was just trying to clarify that it wasn't exactly clear from Zugzug's post how many patients had tinnitus in the first place because he said only 3 tinnitus improvers came from the 15 treated ears. I'm assuming that was just an assumption of his model.Why not just assume that 50% of the participants recruited in the Phase 2A had tinnitus in at least 1 ear?
Yes, completely normal below 5 kHz.Is below 5 kHz completely normal? This could give you a better word score.
I think you likely have losses from 5 kHz all the way up. Your UHF hearing is involved in speech in noise, too, so you don't necessarily need synaptopathy to explain it in your case imo.
For the Nth time, the entire sector is down.Hello friends, anyone else notice that IBB and NASDAQ were both up today but FREQ continues to drop?
You have to wonder if some leaking is going on over there at headquarters and the news is not good. I'm desperate for a solution like the rest of you and have also accumulated 400 shares.
- Feb 14, 2020
- 1,630
- Tinnitus Since
- 1-2019
- Cause of Tinnitus
- 20+ Years of Live Music, Motorcycles, and Power Tools
My bad. Mixed up the convo.I wasn't talking about Phase 2a... am I missing something? I was just trying to clarify that it wasn't exactly clear from Zugzug's post how many patients had tinnitus in the first place because he said only 3 tinnitus improvers came from the 15 treated ears. I'm assuming that was just an assumption of his model.
- May 27, 2020
- 556
- Tinnitus Since
- 2007
- Cause of Tinnitus
- Loud music/headphones/concerts - Hyperacusis from motorbike
1) ETFs containing FREQ re-balanced todayHello friends, anyone else notice that IBB and NASDAQ were both up today but FREQ continues to drop?
You have to wonder if some leaking is going on over there at headquarters and the news is not good. I'm desperate for a solution like the rest of you and have also accumulated 400 shares.
2) Biotech is down in general
3) Traders cashing out the pre-results wave due to cold feet
Nothing to worry about. The good news is that we are through Friday, market has closed and no news came out. If there was a day to announce bad news today would have been it. Perceptive Advisors also own 10% of FREQ and they have a brilliant track record of picking winners.
- May 27, 2020
- 556
- Tinnitus Since
- 2007
- Cause of Tinnitus
- Loud music/headphones/concerts - Hyperacusis from motorbike
I take my previous comment back. This post is officially the best post on Tinnitus Talk of all time.Okay, here is my final deep dive post. I end up computing the 2-sided p-values for all 6 eligible FX-322 participants on the WR test-retest. Recall that 4/6 are statistically significant (and clinically) by the Thornton and Raffin 95% confidence intervals. Hence, we will have 4 individual p-values less than .05 and 2 greater than .05. Note that everyone saw improvement, even if it wasn't statistically significant. One non-significant person was right on the cusp of significant.
Background: I was thinking about the bear/bull divide and it occurred to me where it is. Roughly speaking, since the data was imbalanced by chance, the placebos started off closer to a ceiling effect. Hence, even though all group level differences were statistically significant, except PTA, the bears would argue that the placebos had a harder fight, with higher starting baselines -- probably some validity to this, even though it's percentage based.
But here's where the divide really is. Frequency Therapeutics have said (in the Tinnitus Talk Podcast) that there shouldn't really be a placebo effect with hearing words. Looking at the placebo patients, this is what we would expect. They all land in the 95% confidence intervals and scattered above and below.
The bulls think even with the data imbalance, let's focus on the responders. Placebo control is a little less important to us because we think the placebo effect is less for hearing. We see the 4 WR responders with massive gains and think that even though it's only 4, there's no way that's by chance or just retesting a little better. I think so much of the bull/bear position is what you think of a placebo effect. However, I do want to reiterate that the FX-322 group did outperform the placebo group in every test except one so it's not just zooming in on 4 ears.
Okay, here's my work and calculations from Thornton and Raffin. I am writing it out for completeness, but it's perfectly fine to skip right to the p-values. From the patent submission,
View attachment 44095
By Central Limit Theorem (justified), we apply angular transformations to baseline and day 90 scores. Then using the Freeman and Tukey uniform variance formula that was adjusted by Mosteller and Youtz (1961), we have the formula
Z=(arcsin(sqrt(x/(n+1)))+arcsin(sqrt((x+1)/(n+1)))-(arcsin(sqrt(y/(n+1)))+arcsin(sqrt((y+1)/(n+1))))/sqrt(2/(n+1/2)).
Here,
This leads to the following Z-scores and corresponding 2-sided p-values. Note that alpha=0.05.
- x=# correct out of 50 at baseline,
- y = # correct out of 50 at day 90,
- n=50
Patient 918: Z=-1.8972, p=2*P(Z<-1.8972)= 0.0578,
which is not less than alpha (but close) so not statistically significant.
Patient 932: Z=-0.9795, p=2*P(Z<-0.9795)= 0.3273,
which is not less than alpha and not close.
Patient 919: Z=-2.1268, p=2*P(Z<-2.1268)= 0.0334,
which is less than alpha so statistically significant.
Patient 916: Z=-4.0547, p=2*P(Z<-4.0547)= 0.00005,
which is way less than alpha so very statistically significant.
Patient 936: Z=-3.9133, p=2*P(Z<-3.9133)= 0.00009,
which is way less than alpha so very statistically significant.
Patient 937: Z=-5.0387, p=2*P(Z<-5.0387)= 0.00000047,
which is way less than alpha so very statistically significant.
So I will conclude with some commentary on these p-values. The last three (patients 916, 936, and 937) have very small p-values. It's even crazier because this is two-sided, which produces bigger p-values. The probability of that occurring by chance is practically impossible to believe.
Let's just say that I'm a bull and there are 3 patients in the Phase 1b study riding me hard.
Shut the thread down. See you all in the clinic in 2 years.
Yeah, first time it's bucking the IBB trend this week but there are a lot of potential reasons for this including:Hello friends, anyone else notice that IBB and NASDAQ were both up today but FREQ continues to drop?
You have to wonder if some leaking is going on over there at headquarters and the news is not good. I'm desperate for a solution like the rest of you and have also accumulated 400 shares.
1) Common for people to get nervous and sell before news and the consensus is probably that news will hit around earnings (which is the norm). People get scared of the potential of losing money on bad results whether or not they will occur.
2) Manipulation. Ironically, it could be occurring because people are scared it will go up. Shorts worried about good results and want to keep the price down to protect losses.
If there was a "leak", the stock would move way more than it is imo because computer algos would be following the unusual movement.
Lots of approved drugs had stock drops leading up to readouts. People *always* think there is a leak but that's rarely the case.
Finally, another one reads the signs correctly. There always is leaking in stock companies before publishing study or company results.Hello friends, anyone else notice that IBB and NASDAQ were both up today but FREQ continues to drop?
You have to wonder if some leaking is going on over there at headquarters and the news is not good. I'm desperate for a solution like the rest of you and have also accumulated 400 shares.
 Member
Member